stuff

1-linked-list/README.md

@@ -0,0 +1,35 @@
+Single Linked List
+===========
+
+Wikipedia on [Linked Lists](http://en.wikipedia.org/wiki/Linked_list).
+CS50 on [Linked Lists](https://www.youtube.com/watch?v=5nsKtQuT6E8)
+
+A linked list is a common data structure, where nodes are grouped to form a sequence. Each node holds data and a pointer to another node.
+
+###Visualization
+
+    |42|-> |55|-> |4|-> |39|-> None
+
+A linked last can be advantageous over an array because it is dynamic - to insert or delete a node in the middle of the list, we don't need to re-index the entire list, like an array. We only need to alter a pointer.
+
+For example, to insert `|79|` after `|4|` in the list above, pseudocode would look this:
+
+    79 = new node
+    79.next should point to 4.next (i.e. 4.next points to 39)
+    # after insertion:
+        - 4.next should point to 79
+        - 79.next should point to 39
+        - 39.next should still point to None
+        
+    
+
+###Implementation
+
+Do not use lists or dictionaries. That's cheating. Create this using classes only. You will want a Node class and a LinkedList class.
+
+Create your data structures and the following methods that allow your linked list to:
+- insert
+- search (First iteratively then recursively)
+- delete
+- print backwards
+

1-linked-list/linked-list.py

@@ -0,0 +1,132 @@
+class Node:
+	def __init__( self, payLoad, next=None ):
+		self.payLoad = payLoad
+		self.next = next
+
+class LinkedList:
+	head = None
+	def __init__( self, *args ):
+		for item in args:
+			self.insert( item )
+
+	# allow print to work correctly.
+	# def __str__(self):
+	# 	return self.print()
+
+	# allow += and + operates to work correctly  
+	def __add__( self, item ):
+		self.insert( item )
+
+		return self
+
+	# allow the in operator to work
+	def __iter__(self):
+		current = self.head
+
+		while current:
+			yield current.payLoad
+			current = current.next
+
+	# allow the len() function to be used
+	def __len__( self ):
+		return self.find( None )['count']
+
+	# internal method check if node is a node object
+	def __check_Node( self, node ):
+		if not isinstance(node, Node):
+			return Node(node)
+
+		return node
+
+	def find( self, match ):
+		''' Searches the list for a matching node. If found it will return the
+			current node, last node as Node objects and position as an int.
+			If nothing is found, it will return None, the last node as a Node
+			object, and the full length of the list as an int.
+
+			This function will ONLY return the first match.
+
+			setting match to None will find the end of the list and return the
+			last node as return['last']
+
+			This method does alot of the heavy lifting.
+		'''
+
+		current = self.head
+		last = None
+		count = 0
+
+		while current:
+			if current.payLoad == match:
+				return {'current': current, 'last': last, 'count': count}
+
+			last = current
+			current = current.next
+			count += 1
+
+		return {'current': current, 'last': last, 'count': count}
+
+	def insert( self, item, after=None ):
+		# check to see if adding a whole LinkedList
+		if isinstance(item, self.__class__):
+			self.find(None)['last'].next = item.head
+			return self
+
+		item = self.__check_Node( item )
+
+		# figures out the position of the node
+		previous_node = self.find(after)['current'] if after else self.find(None)['last']
+
+		# if the after node isnt found, do nothing.
+		if not previous_node: return None;
+
+		item.next = previous_node.next
+		previous_node.next = item
+
+		return item
+
+	def print_right( self ):
+
+		def rec( current ):
+			if not current: return 'None'
+			return rec( current.next ) + ' <= ' + current.payLoad
+
+		return( rec( self.head ) + ' <= head' )
+
+	def __str__( self ):
+		current = self.head
+		out = 'head' + ' => '
+
+		while current:
+			out += current.payLoad + ' => '
+			current = current.next
+
+		return out + 'None'
+
+	def __repr__( self ):
+		return self.__str__()
+
+	def delete( self, payLoad ):
+		match, before, count = self.find( payLoad )
+		if match:
+			before.next = match.next
+			return match
+
+		return None
+
+if __name__ == '__main__':
+	l2 = LinkedList('a')
+	l2.insert('b')
+	l2.insert('c')
+	l2 += Node('d')
+	l2.insert('1', 'c')
+	print(l2)
+
+	l = LinkedList( Node('1') )
+	l.insert( Node('2'))
+	l.insert( Node('3'))
+	l.insert( Node('4'))
+	l += Node('5')
+	l.insert('a')
+	l3 = l + l2
+	print( l.print_right() )

1-linked-list/linked_list.py

@@ -0,0 +1,142 @@
+class Node:
+	def __init__(self, payLoad, next=None):
+		self.payLoad = payLoad
+		self.next = next
+
+	def __str__(self):
+		return str(self.payLoad)
+
+	def __repr__(self):
+		return self.__str__()
+
+class LinkedList:
+	def __init__(self, item):
+		self.next = self.next = self.__check_Node(item)
+		self.head = self.next
+
+	def __repr__(self):
+		return self.__str__()
+  
+	def __add__(self, item):
+		'''allow += and + operates to work correctly'''
+		if item is self: return False
+		self.push( item )
+
+		return self
+
+	def __iter__(self):
+		'''allow the in operator to work'''
+		current = self.next
+
+		while isinstance(current, Node):
+			yield current
+			current = current.next
+
+	def __len__(self):
+		'''allow the len() function to be used'''
+		return self.find( None )['count']
+
+	def __str__(self):
+		'''allow print to work correctly'''
+		current = self.next
+		out = 'Head' + ' => '
+
+		for current in self:
+		# while current:
+			out += str(current.payLoad) + ' => '
+			current = current.next
+
+		return out + 'None'
+
+	def __check_Node(self, node):
+		'''internal method check if node is a node object'''
+		if isinstance(node, self.__class__):
+			return node.head
+
+		if not isinstance(node, Node):
+			return Node(node)
+
+		return node
+
+	def find(self, match):
+		''' Searches the list for a matching node. If found it will return the
+			current node, last node as Node objects and position as an int.
+			If nothing is found, it will return None, the last node as a Node
+			object, and the full length of the list as an int.
+
+			This function will **ONLY** return the first match.
+
+			setting match to None will find the end of the list and return the
+			last node as return['last']
+
+			This method does alot of the heavy lifting.
+		'''
+
+		current = self.next
+		last = None
+		count = 0
+
+		while current:
+			if current.payLoad == match:
+				return {'current': current, 'last': last, 'count': count}
+
+			last = current
+			current = current.next
+			count += 1
+
+		return {'current': current, 'last': last, 'count': count}
+
+	def insert(self, *items, after=False):
+
+		# figures out the position of the node
+		previous_node = self.find(after)['current'] if after != False else self
+
+		for item in items[:: -1]:
+
+			if isinstance(item, self.__class__):
+				item = item.next
+
+			item = self.__check_Node( item )
+			item.next = previous_node.next
+			previous_node.next = item
+
+		return self
+
+	def push(self, item):
+		last_node = self.find(None)['last']
+		node = self.__check_Node(item)
+		last_node.next = node;
+
+
+	def print_right(self):
+
+		def rec(current):
+			if not current: return 'None'
+			return rec( current.next ) + ' <= ' + current.payLoad
+
+		return rec( self.next ) + ' <= Head' 
+
+	def delete(self, payLoad):
+		match = self.find( payLoad )
+		if match['current']:
+			match['last'].next = match['current'].next
+			return match['current'];
+
+		return None
+
+if __name__ == '__main__':
+	''' Some testing stuff '''
+	l1 = LinkedList('b')
+	l1.insert('a')
+	l1.push('c')
+
+	print(l1)
+
+	l2 = LinkedList('1')
+	l2.push('2')
+
+	print(l2)
+
+	l1 +=l2
+	print(l1)
+

10-binary-search/README.md

@@ -0,0 +1,51 @@
+Binary Search
+===============
+
+#### Summary
+
+In computer science, a binary search or half-interval search algorithm finds the position of a specified input value (the search "key") within an array **sorted** by key value. For binary search, the array should be arranged in ascending or descending order. 
+
+#### An example
+The next best example I can think of is the telephone book, normally called the White Pages or similar but it'll vary from country to country. But I'm talking about the one that lists people by surname and then initials or first name, possibly address and then telephone numbers.
+
+Now if you were instructing a computer to look up the phone number for "John Smith" in a telephone book that contains 1,000,000 names, what would you do? Ignoring the fact that you could guess how far in the S's started (let's assume you can't), what would you do?
+
+A typical implementation might be to open up to the middle, take the 500,000th and compare it to "Smith". If it happens to be "Smith, John", we just got real lucky. Far more likely is that "John Smith" will be before or after that name. If it's after we then divide the last half of the phone book in half and repeat. If it's before then we divide the first half of the phone book in half and repeat. And so on.
+
+This is called a binary search and is used every day in programming whether you realize it or not.
+
+#### Write your Binary Search
+
+Start at the middle of your dataset.
+If the number or word you are searching for is lower, stop searching the greater half of the dataset. Find the middle of the lower half and repeat.
+
+Similarly if it is greater, stop searching the smaller half and repeat the process on that half. By continuing to cut the dataset in half, eventually you get your index number. 
+
+This is an O(log n) operation, which is generally the fastest search.
+
+#### Write assert statements to test your code
+
+Write six assert statements to test your code. What if the number isn't in the dataset? What happens to your program? Error check and make sure it doesn't crash.
+
+#### Benchmark
+
+Create a new file, and import the following:
+
+Your benchmark function  
+Your linear search
+Your binary tree
+
+Using your benchmark function, benchmark your binary search versus the linear search. Which is faster? What is an advantage of both? Be cool and import the benchmark.py and linear.py file and call them that way. No copy paste. Write in comments in your python file.
+
+Now benchmark your binary search against your binary tree's search function. Which is faster?
+
+
+#### Word List
+
+Import the file "wordlist.txt" and search for some words. Specifically I want the index of 'illuminatingly', 'lexicalisation', and 'unexpectedness'.
+
+Benchmark the binary and linear searches again using this file. 
+
+
+#### Resources
+[Binary Search Algorithm](http://en.wikipedia.org/wiki/Binary_search_algorithm)

10-binary-search/binary-search.py

@@ -0,0 +1,6 @@
+def binary_search():
+  pass
+
+
+##sample dataset
+arr = [1,3,9,11,23,44,66,88,102,142,188,192,239,382,492,1120,1900,2500,4392,5854,6543,8292,9999,29122]

11-benchmark/README.md

@@ -0,0 +1,21 @@
+Benchmarking your Code
+=======================
+
+How fast is your code? Do you want to find out? Yes!
+
+###Write a Benchmark function
+
+Write a Benchmark function that takes the following as inputs:
+
+-the function you want to benchmark  
+- the amount of times you want it to run  
+
+and have your Benchmark function return the total amount of time it took.
+
+The datetime library is imported at the top of the file. Look it up and how it's going to help you solve this problem. Do not import any other libraries.
+
+###Test your Factorial Functions
+
+Test your Iterative Factorial function versus your recursive - which is faster??
+
+Import this file into atleast one other of your assignments today and test some of your functions.

11-benchmark/benchmark.py

@@ -0,0 +1,6 @@
+import datetime
+import imp
+##what is this code doing? figure out how to call your fibonacci functions in this file.
+fibonacci = imp.load_source('fibonacci', '../2-is-fibonacci/fibonacci.py')
+
+def benchmark(func, times):

12-bubble-sort/README.md

@@ -0,0 +1,15 @@
+Bubble Sort
+===========
+
+Wikipedia on [bubble sort](http://en.wikipedia.org/wiki/Bubble_sort).
+
+#### Algorithm
+
+A bubble sort is a sorting algorithm with a Big O complexity of O(n**2). It is called bubble sort, because the small numbers "bubble" to the top of the list.  
+![bubble sort gif](http://upload.wikimedia.org/wikipedia/commons/c/c8/Bubble-sort-example-300px.gif)
+
+The general flow is to step through the list, continually comparing pairs of numbers. If the number on the left is larger than the number on the right, swap them and continue.
+
+#### Implementation
+
+Write a function, `bubble_sort()`, that takes an `list`. It should return a sorted `list`, using the bubble sort algorithm.

12-bubble-sort/bubble_sort.py

@@ -0,0 +1,8 @@
+def bubble_sort(list):
+    pass
+
+
+
+
+assert bubble_sort([5,19,4,1,36,99,2]) == sorted([5,19,4,1,36,99,2])
+assert bubble_sort(["Greg", "Armen", "Ken"]) == sorted(["Greg", "Armen", "Ken"])

13-merge-sort/README.md

@@ -0,0 +1,28 @@
+Merge Sort
+===========
+
+Before you start, watch [this video](https://www.youtube.com/watch?v=EeQ8pwjQxTM) explaining the Merge Sort.
+
+#### Algorithm
+
+To perform the merge sort, first break the list down to sorted lists.
+
+How do we get a sorted list by breaking it down? By making a list containing each individual element. After all, a list with a single value is sorted.
+
+Then, every set of two lists are compared, and merged. For example:
+```py
+[8, 2, 5, 10, 19, 1] ###starting list
+
+[8] [2] [5] [10] [19] [1] ### fully broken down
+
+[2,8] [5, 10] [1,19] ### each set of two compared and merged
+
+[2,5,8,10] [1,19] ### sets further compared and merged
+
+[1,2,5,8,10,19] ### further compared and merged for the finished product
+```
+#### Implementation
+
+Write a function `merge_sort()` that takes an unsorted `list` and using the merge sort algorithm, returns a sorted `list`. Do it recursively.
+
+It is probably a good idea to make a helper function for the initial breaking down of the list.

13-merge-sort/merge_sort.py

@@ -0,0 +1,3 @@
+def merge_sort(arr):
+
+merge_sort([98, 744, 28, 81, 447, 2, 5, 10, 99, 55])

14-quicksort/README.md

@@ -0,0 +1,22 @@
+Quicksort
+=========
+
+Wikipedia on [Quicksort](http://en.wikipedia.org/wiki/Quicksort).  
+
+![quicksort gif](http://upload.wikimedia.org/wikipedia/commons/6/6a/Sorting_quicksort_anim.gif)
+
+#### Algorithm
+
+Another divide-and-conquer algorithm, Quicksort works by picking a pivot point, or a value in the array, and reordering all the elements with values less than the pivot to the front of it, and all values greater than the pivot to the back. This is called the partition operation, and upon completion the pivot point is in its correct position.
+
+You then recursively apply the same steps to each sub array - the elements smaller than the last pivot, and the elements larger than the last pivot.
+
+Your base case is when a sub array is length 1 or 0.
+
+#### The Pivot
+
+Unsure of where to set the pivot? Read under the header "Implementation issues" on the Wikipedia.
+
+#### Implementation
+
+Write a function, `quicksort()` that takes an unsorted `list` and returns a sorted `list`. You may want to use some helper functions to partition.

14-quicksort/quicksort.py

@@ -0,0 +1,9 @@
+def quicksort(list):
+
+
+def assertion(actualAnswer, expectedAnswer):
+    print("Your answer:    " + str(actualAnswer))
+    print("Expcted answer: " + str(expectedAnswer))
+    print(actualAnswer == expectedAnswer)
+
+assertion(quicksort([4, 2, 5, 8, 6]), [2, 4, 5, 6, 8])

2-nested-arrays/README.md

@@ -0,0 +1,41 @@
+Nested Arrays
+=============
+
+###Dynamically create a game board
+
+Dynamically create a sort of game board that appears like so:
+
+	[28, 47, 39, 36]  
+	[3, 41, 46, 1]  
+	[34, 10, 20, 2]  
+	[19, 9, 26, 10]  
+
+Hold this game board inside a GameBoard class. Create board and values inside on instantiation of a GameBoard class object. Use random for the values inside.
+
+###First Method - Print Board
+Create an instance method that prints the whole board, similarly to how it is presented above.
+
+###More Methods
+
+Create four more instance methods- getRow(), getCol(), getCoords() and getSurround()
+
+getRow should take a row numbers (starting at the top from 0) and return the row. For the example above:
+
+		board.getRow(1) >>> 3,41,46,1  
+
+getCol should take a col number (starting at the left from 0) and should return the column. For the example above:
+
+		board.getCol(2) >>> 39, 46, 20, 26
+
+getCoords should take a number on the board, and check for its existence. If it does exist, it should return the row and column.
+
+		board.getCoords(9) >>> (3, 1)  
+		board.getCoords(10) >>> (2, 1) #returns the first one it finds
+		board.getCoords(99) >>> False
+
+getSurround should take the row and column coordinates and return all surrounding values, or more specifically, values of all the coordinates that touch the input coordinates.
+
+		board.getSurround(1,1) >>> 28, 37, 39, 46, 20, 10, 34, 3
+		board.getSurround(0,3) >>> 1, 46, 39
+
+

2-nested-arrays/nested-arrays.py

@@ -0,0 +1,3 @@
+import random
+
+

3-text-adventure/README.md

@@ -0,0 +1,78 @@
+Text Adventure
+===============
+
+For this challenge we'll be programming a videogame called "The Adventure of the Barren Moor".
+
+In "The Adventure of the Barren Moor" the player is in the middle of an infinite grey swamp. This grey swamp has few distinguishing characteristics, other than the fact that it is large and infinite and dreary. 
+
+However, the player DOES have a magic compass that tells the player how far away the next feature of interest is. The player can choose north, south, east or west every move towards the feature.
+
+Here is an example playthrough:
+
+		You awaken to find yourself in a barren moor.  Try "look"
+
+`>look`
+
+		Grey foggy clouds float oppressively close to you, 
+		reflected in the murky grey water which reaches up your shins.
+		Some black plants barely poke out of the shallow water.
+
+		Try "north","south","east",or "west"
+
+		You notice a small watch-like device in your left hand.  
+		It has hands like a watch, but the hands don't seem to tell time. 
+
+
+		The dial reads '5m'
+
+`>north`
+
+		The dial reads '4.472m'
+`>north`
+
+		The dial reads '4.123m'
+`>n`
+
+		The dial reads '4m'
+`>n`
+
+		The dial reads '4.123m'
+`>south`
+
+		The dial reads '4m'
+`>e`
+
+		The dial reads '3m'
+`>e`
+
+		The dial reads '2m'
+
+`>look`
+	
+		Grey blackness as far as the eye can see.
+
+`>e`
+
+		The dial reads '1m'
+`>e`
+
+		You see a box sitting on the plain.
+
+		The dial reads '0m'
+
+`look` 
+
+		The box is filled with treasure!  You win!  The end.
+
+
+#### First Iteration
+
+Write the game to play as it does above. The player's starting location should be randomly generated, as well as the point of interest's location.
+
+When the player reaches the point of interest, the game ends.
+
+#### Second Iteration
+
+Create the necessary data for two more points of interest. In addition to the location of the point of interest being randomly generated, the data should be as well. 
+
+When the player reaches the point of interest, another one should be generated and the "magic compass" should guide the player there.

4-stack/README.md

@@ -0,0 +1,40 @@
+Stack
+=====
+
+Wikipedia on [stacks](http://en.wikipedia.org/wiki/Stack_(abstract_data_type)).  
+
+Similarly, the Linked List, a stack is an abstract data type. It is LIFO, or Last In First Out. Each node holds data and a pointer to the next node.
+
+###Visualization
+
+		|42|
+		 |
+		|60|
+		 |
+		|99|
+		 |
+		|3|
+		 |
+		None
+
+The main operations available to the Stack are push and pop. 
+- Pop should remove the top node and return it. 
+- Push should add to the top of the stack.
+
+###Methods
+
+Create your datatypes and create the following methods:
+
+- push - adds to the stack
+
+- pop - removes from the top of the stack
+
+- peek - Find the item at the top of the stack
+
+- empty - Is the stack empty?
+
+###Additional Methods
+
+In the wikipedia article, read under the title "Hardware Stacks". Emulating a hardware stack, add the operations it lists to your class. This is open ended and implementation is up to you.
+
+

4-stack/stack.py

@@ -0,0 +1,3 @@
+class Stack:
+    def __init__():
+    	pass

5-queue/README.md

@@ -0,0 +1,29 @@
+## Queue
+
+Wikipedia on [queues](http://en.wikipedia.org/wiki/Queue_(abstract_data_type)).
+
+The opposite of the Stack, the Queue is a FIFO data structure - First In, First Out.
+
+#### Visualization
+
+A music playlist works like a queue. 
+
+		|Tommy Tutone - 8675309 Jenny|
+				|
+		|Europe - The Final Countdown|
+				|
+		|Dio - Holy Diver|
+
+The enqueue operation will add a song to the end. The dequeue operation will pop off the front.
+
+#### Implementation
+
+You will need to create a Queue class that holds the following methods: 
+
+- enqueue
+
+- dequeue 
+
+- is_empty 
+
+- get_front.

5-queue/queue.py

@@ -0,0 +1,3 @@
+class Queue:
+    def __init__():
+    	pass

6-binary-search-tree/README.md

@@ -0,0 +1,26 @@
+## Binary Search Tree
+
+Wikipedia on [Binary Search Tree](http://en.wikipedia.org/wiki/Binary_search_tree)
+
+A binary search tree is a node based binary tree data structure. It is ordered in a particular way, where all values to the left of a node must be lower and all values to the right of a node must be higher relative to the root node aka the top node
+
+#### Visualization
+
+![binary search tree](http://upload.wikimedia.org/wikipedia/commons/thumb/d/da/Binary_search_tree.svg/200px-Binary_search_tree.svg.png)
+
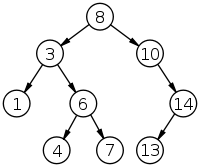
+Like the linked list, each node holds pointer to other nodes. In this case, each node has two pointers - a left and a right.
+
+#### Implementation
+You will create two classes:
+  - `TreeNode`
+    - instantiate it with a value, as well as properties named left and right to hold other nodes.
+  - `Tree`
+    - instantiate it with a root node.
+
+#### Methods
+
+You will create the following methods for your Tree class:
+  - `preorder`: this will traverse the tree and print every node's value
+  - `search`: a recursive function that searches the tree for the value. Returns True if node exists, else returns False
+  - `insert`: this should correctly insert a TreeNode in proper place (i.e.)
+  - `inorder`: function that prints every node's value **in order** from lowest to highest

6-binary-search-tree/bst.py

@@ -0,0 +1,7 @@
+class Tree:
+	def __init__(self, root_node):
+		pass
+
+class Node:
+	def __init__(self):
+		pass

8-insertion-sort/README.md

@@ -0,0 +1,24 @@
+Insertion Sort
+==============
+
+Wikipedia on [insertion sort](http://en.wikipedia.org/wiki/Insertion_sort).
+
+![insert sort gif](http://upload.wikimedia.org/wikipedia/commons/0/0f/Insertion-sort-example-300px.gif)
+
+#### Algorithm
+
+Insertion sort is a common sorting algorithm that, while still its worst case is still O(n**2), it is much more efficient than Bubble sort on average.
+
+According to wikipedia, when people manually sort something, like a deck of cards for example, most use a method similar to insertion sort.
+
+The algorithm is simple - here it is in pseudocode.
+```
+from i = 1 to length of array:
+	j = i
+	while j > 0 and array[j-1] > array[j]:
+		swap array[j] and array[j-1]
+		j = j - 1
+```
+#### Implementation
+
+Write a function `insertion_sort()` that takes an unsorted `list` and returns a sorted `list`, using the insertion sort algorithm.

8-insertion-sort/insertion_sort.py

@@ -0,0 +1,8 @@
+def insertion_sort(arr):
+    pass
+
+
+
+
+assert insertion_sort([5,19,4,1,36,99,2]) == sorted([5,19,4,1,36,99,2])
+assert insertion_sort(["Greg", "Armen", "Ken"]) == sorted(["Greg", "Armen", "Ken"])

9-linear-search/README.md

@@ -0,0 +1,15 @@
+## Linear Search
+
+Write a linear search. Start at the front or the back of the array and iterate through until you find the item you're searching for. 
+
+You can use any method of your choice to accomplish this. 
+
+#### Things to consider
+
+As you're coding, ask yourself...
+* What is the expected Big-O of this search?
+* Do I understand this algorithm?
+* Could I explain it to a 5 year old in less than 5 sentences?
+
+#### Resources
+- [Linear Search](http://en.wikipedia.org/wiki/Linear_search)

9-linear-search/linear.py

@@ -0,0 +1,5 @@
+def linear_search(dataset):
+  pass
+
+
+arr = [1,3,9,11,23,44,66,88,102,142,188,192,239,382,492,1120,1900,2500,4392,5854,6543,8292,9999,29122]